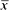 )
gibt den Durchschnittswert der Ergebnisse an (wie viele Phraseologismen kennen
die Probanden im Durchschnitt?) und errechnet sich aus der Summe aller Ergebnisse
geteilt durch die Anzahl der Ergebnisse:[13]
)
gibt den Durchschnittswert der Ergebnisse an (wie viele Phraseologismen kennen
die Probanden im Durchschnitt?) und errechnet sich aus der Summe aller Ergebnisse
geteilt durch die Anzahl der Ergebnisse:[13]Empirische Datenerhebungen gehen in der Regel mit statistischen Darstellungs- und Auswertungsmethoden einher. Umfrageergebnisse werden anhand von Höchst-, Mindest- und Durchschnittswerten und mit Hilfe von Tabellen und Graphiken dargestellt. Dies nicht von ungefähr, stellt die Statistik doch Mittel bereit, einerseits die Erhebungsdaten zu ordnen und übersichtlich darzustellen, anderseits gewisse Regelmäßigkeiten des Korpus nachzuweisen und möglichst Verallgemeinerungen von der untersuchten auf die Gesamtgruppe vorzunehmen.
In vielen wissenschaftlichen Disziplinen, in denen mit empirischen Daten gearbeitet wird - dazu zählen u. a. die Natur- und Sozialwissenschaften -, werden standardisierte quantitative Methoden während der Ausbildung vermittelt und ihre Beherrschung wird in der Forschung als selbstverständlich vorausgesetzt.
In der Sprachwissenschaft haben sich bisher vor allem Bereiche, die den Sozialwissenschaften nahe stehen, wie beispielsweise die Soziolinguistik, um standardisierte Vorgehensweisen bei der Datenerhebung und -auswertung bemüht.
Seit den 1990er Jahren haben sich in der Phraseologie Befragungen auch in der deutschen Forschung als gängige Methode zur Gewinnung korpus- wie probandenorientierter Daten durchgesetzt.[1] Die generelle Notwendigkeit statistischer Auswertungsmethoden wurde für phraseologische Fragestellungen sowohl theoretisch herausgestellt[2] als auch in verschiedenen Arbeiten praktisch aufgezeigt.[3] Die statistischen Methoden werden aber während des Studiums in aller Regel nicht vermittelt und ihre Aneignung und Anwendung bleibt in der Forschung dem Einzelnen überlassen. Von einer Standardisierung kann hier noch nicht die Rede sein. Es verwundert daher nicht, dass die empirischen phraseologischen Arbeiten der letzten 15 Jahre methodologisch sowohl bei der Gestaltung der Befragung als auch, und dies in weit größerem Maße, bei der Auswertung der Umfrageergebnisse sehr große Unterschiede aufweisen.
Die divergierenden Ergebnisse, beispielsweise zum Einfluss des Geschlechts oder des Bildungsstands auf die Sprichwortkenntnis, lassen sich zum Teil auf die Nichtbeachtung von Testvoraussetzungen, d. h. beispielsweise zu geringe Probandenzahlen und/oder eine fehlende Repräsentativität der Teilnehmer für die angestrebte Gesamtgruppe, zum Teil auch auf die unsachgemäße Anwendung statistischer Tests zurückführen.
Ziel des vorliegenden Artikels ist es, zugeschnitten auf phraseologische Befragungen[4] einen eingängigen und möglichst klar verständlichen Überblick über die korrekte Auswahl und Durchführung einiger grundlegender statistischer Tests zu geben sowie auf die Notwendigkeit der Berücksichtigung von Interaktionen zwischen den verschiedenen Faktoren (d. h. ihre gegenseitige Beeinflussung) hinzuweisen.
Zugunsten der Verständlichkeit wurde möglichst auf mathematische Details verzichtet. Für weitergehende Informationen empfiehlt es sich, entsprechende Statistikbücher zu konsultieren. Im Bereich der Sprachwissenschaft sind diese allerdings bisher relativ dünn gesät (cf. Albert/Koster 2002 und Schlobinski 1996). Rein statistische Fachliteratur andererseits behandelt die für diese praktischen Zwecke benötigten Tests z. T. eher stiefmütterlich.[5] Es sei daher explizit auf die Literatur anderer Fachbereiche, z. B. aus den Naturwissenschaften, der Psychologie oder Soziologie, verwiesen, die die angewandte Statistik sehr viel ausführlicher und anschaulicher darstellen und mit zahlreichen Fallbeispielen illustrieren (cf. Köhler/Schachtel/Voleske 1996, Wirtz/Nachtigall 1998 und Nachtigall/Wirtz 1998, Atteslander 2003). In der fortgeschrittenen Statistik ist das Hinzuziehen eines anwendungsorientierten Statistikers am besten bereits vor Beginn der Datenerhebung auf jeden Fall empfehlenswert.
In diesem Sinne möge deutlich werden, dass die Statistik auch bei empirischen phraseologischen Fragestellungen als Darstellungshilfe und zur Prüfung von Hypothesen unerlässlich ist.
Die Zielsetzungen empirischer phraseologischer Untersuchungen lassen sich in zwei Gruppen gliedern:
Zur ersten Gruppe zählen Arbeiten, deren Ziel die Beschreibung empirischer Daten zu einem Korpus oder den Probanden ist. Ihr Schwerpunkt liegt entweder auf der aktuellen Bekanntheit und/oder Verwendung der im Korpus enthaltenen Phraseologismen und/oder deren Varianten oder auf der Beschreibung eines Prozesses (z. B. Spracherwerb). Diese Fragestellungen sollen hier als eindimensional bezeichnet werden, da sie sich auf die Betrachtung einer Ebene, nämlich die des Korpus oder eines Prozesses beschränken.
Im deutschen Sprachraum wurden eindimensionale korpus- oder phraseologismusorientierte Untersuchungen bisher mit dem Ziel durchgeführt, einen lexikalischen Beitrag zu liefern (d. h. Phraseologismen zu beschreiben, cf. Piirainen 2003 zur arealen Verbreitung im deutschsprachigen Raum und 2005 zur arealen Verbreitung im europäischen Sprachraum) oder um ein phraseologisches Minimum bzw. Optimum für den DaF-Unterricht zur Verfügung zu stellen (d. h. Phraseologismen unter einem bestimmten Gesichtspunkt zusammenzustellen, cf. Hallsteinsdóttir/Šajánková/Quasthoff[6] in diesem Band).
Eindimensionale probandenorientierte Untersuchungen stammen aus dem Bereich der Psycholinguistik, in der es beispielsweise darum geht, den Prozess des Spracherwerbs zu beschreiben (cf. Buhofer 1980 oder in ihrer Nachfolge Dürring 2004).
Die zweite Gruppe stellen Arbeiten dar, die die empirisch gewonnenen Daten zum Korpus[7] zu einer anderen Größe in Beziehung setzen. Diese Arbeiten gehen ebenfalls von der aktuellen Bekanntheit und/oder Verwendung der im Korpus enthaltenen Phraseologismen und/oder deren Varianten aus, setzen diese aber zu individuellen Daten der in der Befragung angesprochenen Probanden in Beziehung. Diese Vorgehensweise soll, je nachdem wie viele Faktoren untersucht werden, als zwei- oder mehrdimensional bezeichnet werden.
Häufig wurden im deutschen Sprachraum auf diese Weise soziologische Probandendaten wie Alter, Wohnort, Geschlecht, Ausbildung erfasst und ihr Einfluss auf die Bekanntheit von Phraseologismen geprüft (cf. Grzybek 1991, Häcki Buhofer/Burger 1994, Ďurčo 2003, Juska-Bacher 2006a).
Seltener ist die Erhebung und Auswertung psycholinguistischer Daten (cf. Häcki Buhofer/Burger 1990).
Die Entscheidung für eine beschreibende oder mehrere Faktoren in Beziehung setzende Untersuchung bestimmt die Auswertungsmethode einer Befragung. Eindimensionalität wird qualitativ, evtl. unter Zuhilfenahme von Methoden der deskriptiven Statistik (cf. Abschnitt 3.1), und Zwei- oder Mehrdimensionalität quantitativ, d. h. in Form einer Überprüfung von Hypothesen mit Hilfe der schließenden Statistik untersucht (cf. Abschnitt 3.2). Die statistischen Möglichkeiten werden im folgenden Abschnitt vorgestellt.
Die Statistik versteht die empirisch erhobenen Daten als Stichprobe oder Testgruppe, von der aus sie allgemeine Gesetzmäßigkeiten abzuleiten, d. h. Rückschlüsse auf die Gesamtgruppe zu ziehen versucht (z. B. von der Phraseologismenkenntnis der Probandengruppe auf die Kenntnis der Gesamtgruppe der Muttersprachler). Aus diesem Grund muss die Stichprobe im Hinblick auf die Gesamtgruppe repräsentativ sein, d. h. die Zusammensetzung der Gesamtgruppe widerspiegeln.[9]
Diese Anforderung stellt in der Praxis häufig ein Problem dar, da sie nur durch eine schwierig zu realisierende, streng zufällige Auswahl der Probanden ohne Bevorzugung bzw. Benachteiligung von Gruppen zu erfüllen ist.[10] Man beschränkt sich daher in der Praxis häufig auf die Forderung, dass die Probanden zumindest hinsichtlich der zu untersuchenden Faktoren breit gestreut sein müssen, d. h. wenn im deutschen Sprachraum untersucht werden soll, welchen Einfluss das Alter und der Wohnort auf die Kenntnis von Phraseologismen haben, muss nachgewiesen werden, dass die Probanden zumindest hinsichtlich der untersuchten Faktoren (z. B. Alter und Wohnort) breit gestreut sind (in diesem Fall reicht z. B. eine Befragung von Studenten einer Universität nicht aus). Dabei ist nicht eindeutig definiert, was unter breit gestreut zu verstehen ist. Es liegt im Ermessen des Untersuchenden, die Methoden nach bestem Wissen und Gewissen zu wählen, so dass eine ausreichende Streuung der Probanden gewährleistet ist. Weiterhin ist es wichtig, dass die Methoden der Auswahl und die Probandendaten deutlich und nachvollziehbar offen gelegt werden, damit sich andere ein Bild von der Repräsentativität der Studie machen können.
Zugunsten der Repräsentativität empfiehlt es sich, eine möglichst große Stichprobe anzustreben. Eine große Stichprobenzahl kann zwar die Repräsentativität nicht garantieren, ermöglicht sie aber besser als eine kleine Stichprobengröße, die (fast) nie repräsentativ ist. Eine große Stichprobengröße ist besonders für die schließende Statistik wichtig (cf. t-Test, Varianzanalyse).
Bei jeder empirischen Untersuchung sollte schließlich nicht nur der Mittelwert, sondern auch die Streuung der Ergebnisse besondere Beachtung finden und dokumentiert werden, wenn die Zuverlässigkeit der Schlussfolgerungen gewährleistet werden soll. Die Streuung gibt an, in welchem Bereich typischerweise die Resultate einer Versuchsperson liegen bzw. zu erwarten sind.
Sollen Rückschlüsse nicht nur von der Test- auf die Gesamtgruppe, sondern auch vom untersuchten Korpus auf den gesamten Phraseologismenbestand gezogen werden, so muss auch die Repräsentativität des Korpus gewährleistet sein.
Die im Folgenden angegebenen Beispiele sind rein hypothetisch und dienen nur der Illustration. Für die Berechnung der Maßzahlen und die verschiedenen Tests kann bei der Autorin eine EXCEL-Arbeitsmappe mit Beispielen zu diesem Artikel anfordert werden (britta.juska-bacher@access.unizh.ch bzw. bjuskabacher@hotmail.com). Zu einem konkreten Forschungsprojekt, in dem die hier dargestellten statistischen Methoden Anwendung finden cf. Juska-Bacher (2006a).
Die deskriptive oder beschreibende Statistik fasst empirisch erhobene Daten zusammen und stellt sie anhand von Tabellen, Grafiken und/oder charakteristischen Maßzahlen dar. Die Darstellung der Ergebnisse anhand von Tabellen und Grafiken (z. B. Histogramm, Kreisdiagramm), ist weit verbreitet und soll in diesem Artikel nicht weiter besprochen werden. Zu den sog. Maßzahlen zählen die für die Auswertung einer empirischen phraseologischen Befragung wichtigen Werte, der Mittelwert und die Standardabweichung, die im Folgenden vorgestellt und anhand eines praktischen Beispiels berechnet werden. Für ausführlichere Erklärungen sei auf die im Literaturverzeichnis angegebenen Statistikbücher verwiesen.
Beispiel für die Berechnung von Mittelwert und Standardabweichung:[11]
Eine Befragung zur Bekanntheit der in einer Untersuchung festgestellten 100 bekanntesten Phraseologismen hat folgendes Ergebnis geliefert:
Von 5 befragten Probanden[12] kannten
1 Proband 95,
1 Proband 90,
2 Probanden 89 und
1 Proband 87 Phraseologismen.
Der Mittelwert (oder das arithmetische Mittel; 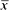 )
gibt den Durchschnittswert der Ergebnisse an (wie viele Phraseologismen kennen
die Probanden im Durchschnitt?) und errechnet sich aus der Summe aller Ergebnisse
geteilt durch die Anzahl der Ergebnisse:[13]
)
gibt den Durchschnittswert der Ergebnisse an (wie viele Phraseologismen kennen
die Probanden im Durchschnitt?) und errechnet sich aus der Summe aller Ergebnisse
geteilt durch die Anzahl der Ergebnisse:[13]
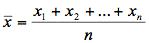
Das heißt für unser Beispiel:
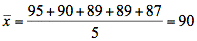
Im Durchschnitt kennen die Probanden 90 Phraseologismen dieses Korpus.
Die Standardabweichung ( s ) gibt die durchschnittlichen Abweichungen der Ergebnisse vom Mittelwert, d. h. ihre Streuung, an und errechnet sich aus der Wurzel der Abweichungsquadrate (Abweichungen vom Mittelwert ins Quadrat) geteilt durch die Anzahl der Ergebnisse minus 1 oder als Formel:
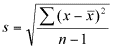
Das heißt für unser Beispiel:
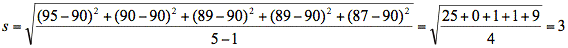
Dieser Wert vermittelt einen Überblick über die Datenverteilung um den Mittelwert. Die Mehrzahl der Ergebnisse sollte sich im Intervall von ± einer Standardabweichung um den Mittelwert befinden, d. h. in diesem Fall im Bereich von [87:93]. Ein Blick auf die Rohdaten zeigt, dass dies tatsächlich der Fall ist: 4 von 5 Werten liegen in dem Bereich einer Standardabweichung um den Mittelwert. Ein hoher Wert für die Standardabweichung bedeutet, dass viele Ergebnisse weit vom Mittelwert entfernt sind, ein geringer Wert, dass die meisten Ergebnisse dicht um den Mittelwert herum liegen.[14]
Die quadrierte Standardabweichung ergibt die sogenannte Varianz (s2)[15], die einen wichtigen Wert in der schließenden Statistik darstellt, für die beschreibende Statistik allerdings von untergeordneter Bedeutung ist:
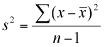
Das heißt für unser Beispiel:
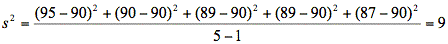
Wenn bei der Durchführung der im folgenden Abschnitt zur schließenden Statistik beschriebenen Tests ein Tabellenkalkulations- oder Statistikprogramm zur Hilfe genommen wird, werden diese Werte in der Regel automatisch vom Programm errechnet.
Die Aufgabe der hier vorgestellten Darstellungsmethoden und Werte dient der anschaulichen Beschreibung (in Form von Tabellen oder Grafiken) bzw. der genauen Charakterisierung (Mittelwert, Standardabweichung) der in einer Befragung erhobenen Daten und unterscheidet sich grundlegend von der schließenden Statistik, indem die beschreibende Statistik keine Vergleiche zwischen verschiedenen Gruppen erlaubt. Die deskriptive Statistik beschreibt einzelne Datengruppen oder Variablen, kann diese aber nicht zueinander in Beziehung setzen und bleibt damit eindimensional. Aus einem Untersuchungsergebnis, das besagt, dass Frauen 75 % und Männer 70 % eines Phraseologismenkorpus kennen, kann man beispielsweise nicht ableiten, dass Frauen generell mehr Phraseologismen kennen als Männer. Für derartige Vergleiche benötigt man die Tests der schließenden Statistik.
Die schließende Statistik setzt mindestens zwei Variablen (z. B. die Bekanntheit von Phraseologismen einerseits und andererseits das Wohnland, z. B. Schweiz, Österreich oder Deutschland) zueinander ins Verhältnis und untersucht den Einfluss einer oder mehrerer unabhängiger Variablen[17] (in diesem Fall das Wohnland) auf die abhängige Variable (in diesem Fall die Bekanntheit der Phraseologismen). Sie geht also zwei- oder mehrdimensional vor. Die schließende Statistik quantifiziert diesen Einfluss anhand von Irrtumswahrscheinlichkeiten, indem sie berechnet, mit welcher Wahrscheinlichkeit der beobachtete Unterschied zwischen den Gruppen (hier also die unterschiedliche Sprichwortkenntnis von Schweizern, Österreichern und Deutschen) zufällig bei einer Befragung auftreten würde, wenn die Teilnehmer in Wirklichkeit die gleiche Sprichwortkenntnis hätten. Sie erlaubt auf diesem Weg eine objektive Überprüfung von Hypothesen, die den Ausgangspunkt einer jeden statistischen Untersuchung bilden.
Beispiel:
Den Ausgangspunkt bildet die Hypothese, dass Schweizer mehr Phraseologismen kennen als Österreicher.
Die Auswertung einer Befragung ergibt, dass die Schweizer Probanden tatsächlich mehr Phraseologismen eines vorgegebenen Korpus kennen. Das mit Hilfe von Methoden der schließenden Statistik erhaltene Testergebnis zeigt eine Irrtumswahrscheinlichkeit (p, aus dem Englischen "probability") von 0,02 = 2 % an, d. h. die Wahrscheinlichkeit, dass die unterschiedlichen Ergebnisse auf einen Zufall zurückzuführen sind, beträgt 2 %.
In der Regel wird eine Irrtumswahrscheinlichkeit p < 0,05 (= 5 %) als signifikanter Unterschied gewertet, d. h. die Wahrscheinlichkeit, dass die beobachteten Unterschiede auf einen Zufall zurückzuführen sind, sollte kleiner sein als 5 %, oder anders ausgedrückt in weniger als einem von 20 Fällen vorkommen.[18] Eine Irrtumswahrscheinlichkeit von p < 0,001 (= 0,1 %, einer von 1000 Fällen) gilt als hochsignifikant.
Im obigen Beispiel würde daher ein statistisch abgesicherter, d. h. signifikanter Unterschied zwischen der Sprichwortkenntnis der Schweizer und der österreichischen Probanden vorliegen. Unter der Voraussetzung, dass eine ausreichend große Anzahl Probanden an der Befragung teilgenommen hat und diese für die drei Bevölkerungsgruppen repräsentativ waren (Kap. 3), kann hinsichtlich dieses Korpus auf eine größere Bekanntheit der Phraseologismen in der Schweiz als in Österreich geschlossen werden. Dabei beträgt die Wahrscheinlichkeit, dass man sich mit dieser Schlussfolgerung irrt, dem statistischen Test zufolge 2 %.
Um signifikante Unterschiede feststellen zu können, ist es vorteilhaft, mit möglichst großen Probandenzahlen zu arbeiten. Selbst wenn sich zwei Gruppen in der Realität unterscheiden, gelingt der Nachweis des Unterschieds mit wenigen Probanden häufig nicht, weil statistische Tests für kleine Probandengruppen einen sehr viel größeren Unterschied verlangen, um eine Signifikanz auszuweisen.[19]
Ein weiterer Grund, der für eine große Stichprobe spricht, ist, dass es sich in der schließenden Statistik i. d. R. um angenäherte Tests mit geschätzten Irrtumswahrscheinlichkeiten handelt, d. h. sie vergleichen eine Stichprobe mit einer theoretischen Idealverteilung. Das Ergebnis ist dabei um so wirklichkeitsgetreuer, je größer die Stichprobe ist.[20]
Im Folgenden werden die vier Tests der schließenden Statistik vorgestellt, die für die Auswertung einer empirischen phraseologischen Untersuchung am wichtigsten erscheinen. Die Wahl des jeweiligen Tests ist dabei nicht beliebig, sondern streng von der Fragestellung der Untersuchung und der Art der erhobenen Daten abhängig.
In der Regel sollten vor der Erhebung des empirischen Materials nicht nur die relevanten Fragestellungen, sondern auch die Methoden der statistischen Auswertung festgelegt werden, um sicherzugehen, dass das erhobene Material die Voraussetzungen für die statistischen Tests erfüllt (z. B. hinsichtlich der Art der Daten, der Stichprobengröße und der Unabhängigkeit der Probanden).
Wie oben bereits angedeutet, arbeitet die schließende Statistik mit abhängigen und unabhängigen Variablen. Eine unabhängige Variable wird während der Untersuchung systematisch variiert bzw. kontrolliert (z. B. das Alter oder der Wohnort der Probanden, da diese vom Untersuchenden frei gewählt werden können, z. B. junge und alte Probanden, die entweder in Österreich, der Schweiz oder in Deutschland wohnen sollen), um ihren Einfluss auf die abhängige Variable (z. B. die Phraseologismenkenntnis) zu prüfen[21].
Die Auswahl des anzuwendenden statistischen Tests hängt, wie oben bereits erwähnt, von der Art der Daten oder genauer vom Skalenniveau der abhängigen und der unabhängigen Variablen ab. Die zwei Skalierungen, die im Zusammenhang mit phraseologischen empirischen Untersuchungen in den weitaus meisten Fällen von Bedeutung sind, sind:
Nominalskalierte Daten
Die gemessenen Daten werden einer von mindestens zwei Kategorien zugeordnet (Entweder-oder-Entscheidung, z. B. bekannt - nicht bekannt oder Wohnland: Schweiz - Österreich - Deutschland oder Geschlecht: Mann - Frau). Es wird die Vorkommenshäufigkeit der verschiedenen Kategorien bestimmt (z. B. den Männern waren 80 von 100 Sprichwörtern bekannt, d. h. 20 waren nicht bekannt, bei den Frauen waren es 85 von 100, die bekannt waren, d. h. 15 waren nicht bekannt).
Intervallskalierte Daten
Die Merkmale werden in gleiche Intervalle unterteilt, denen die gemessenen Daten zugeordnet werden (z. B. absolute Zahlen oder Prozentzahlen: Alter der Probanden in Jahren, Sprichwortkenntnis in %).[22]
Die zentrale Frage für die Auswahl des Tests ist:
Handelt es sich bei der abhängigen und der unabhängigen Variable jeweils um nominal- oder intervallskalierte Daten?
Welcher Test bei welcher Skalenniveau-Kombination zu wählen ist, zeigt Tabelle 1.
|
Abhängige Variable (Was wird gemessen?) |
|||
|
nominalskaliert (z. B. Phraseologismenkenntnis |
intervallskaliert (z. B. Phraseologismenkenntnis: |
||
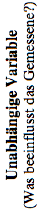 |
Nominalskaliert (z. B. Geschlecht |
Chi-Quadrat-Test |
2 Datengruppen: t-Test mehr als 2 Datengruppen: Varianzanalyse |
|
Intervallskaliert (z. B. Alter |
Logistische Regression[23] |
Regressionsanalyse |
|
Tabelle 1: Zur Wahl des Tests in der schließenden Statistik
Bei der folgenden Beschreibung der Tests wird darauf verzichtet, die Formeln für eine manuelle Durchführung der einzelnen Tests anzugeben (Ausnahme: Chi-Quadrat-Test), da diese in der Regel mit Hilfe von Computerprogrammen berechnet werden. Aufgrund der weiten Verbreitung von EXCEL und der Vertrautheit vieler Benutzer mit diesem Programm wird die Durchführung der Tests in EXCEL[24] beschrieben. Selbstverständlich kann auch auf spezielle Statistikprogramme wie SPSS oder andere zurückgegriffen werden.
Chi-Quadrat-Test
Der Chi-Quadrat-Test (auch: Kontingenztest) untersucht die Frage, ob es eine Beziehung zwischen zwei nominalskalierten Variablen gibt (z. B. zwischen der abhängigen Variablen Phraseologismenkenntnis und der unabhängigen Variablen Geschlecht). Der Chi-Quadrat-Test ist der einzige der hier vorgestellten Tests, der leider nicht direkt in EXCEL implementiert ist. Er kann aber trotzdem unter Verwendung der genannten Formeln mühelos in EXCEL (oder in einem Statistikprogramm) berechnet werden.
Beispiel:
Geprüft werden soll die Hypothese, dass mehr Frauen einen bestimmten Phraseologismus kennen als Männer. Dafür werden anhand eines Fragebogens 100 Männer und 100 Frauen befragt. Die Umfrage ergibt hinsichtlich eines Phraseologismus, dass er 80 Männern und 90 Frauen bekannt ist.[25]
Die erfragten oder beobachteten Werte werden in einer sog. Kontingenztabelle festgehalten, die auch die Zeilen- und Spaltensumme angibt.
|
bekannt |
nicht bekannt |
Zeilensumme |
|
|
Frauen |
90 |
10 |
90 + 10 = 100 |
|
Männer |
80 |
20 |
80 + 20 = 100 |
|
Spaltensumme |
90 + 80 = 170 |
10 + 20 = 30 |
N = 200 |
Tabelle 2: Beobachtungswerte zum Chi-Quadrat-Test-Beispiel
Beim Chi-Quadrat-Test wird mit absoluten Häufigkeiten, nicht mit Prozenten gerechnet. Dieser Test setzt die beobachteten Häufigkeiten zu den erwarteten Werten in Beziehung. Die beobachteten Häufigkeiten sind der Kontingenztabelle zu entnehmen. Die erwarteten Werte sind die Werte, die auftreten würden, wenn beide Probandengruppen den Phraseologismus gleich häufig kennen würden. Die Erwartungswerte für jeden der vier Tabelleneinträge berechnen sich aus der Zeilensumme multipliziert mit der Spaltensumme und geteilt durch die Gesamtzahl der Probanden (N):[26]

In unserem Fall ergeben sich folgende Erwartungswerte:
|
bekannt |
nicht bekannt |
Zeilensumme |
|
|
Frauen |
100*170/200=85 |
100*30/200=15 |
100 |
|
Männer |
100*170/200=85 |
100*30/200=15 |
100 |
|
Spaltensumme |
170 |
30 |
N = 200 |
| Tabelle 3: | Erwartungswerte zum Chi-Quadrat-Test-Beispiel. Man beachte, dass sich die Zeilen- und Spaltensummen im Vergleich zu den Beobachtungswerten nicht ändern. |
Der Chi-Quadrat-Wert (x 2) berechnet sich nun aus der Summe der quadrierten Abweichungen aller Tabelleneinträge geteilt durch ihren jeweiligen Erwartungswert oder in einer Formel:
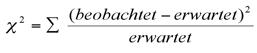
In unserem Fall gilt:
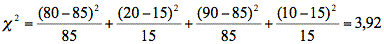
Für die Beurteilung der Signifikanz dieses x 2-Wertes werden die sogenannten Freiheitsgrade[27] benötigt, die sich für den Chi-Quadrat-Test aus der (Anzahl der Spalten minus 1) multipliziert mit der (Anzahl der Zeilen minus 1) errechnen, in unserem Beispiel mit 2 Zeilen und 2 Spalten heißt das also (2 - 1)*(2 - 1) = 1 Freiheitsgrad. Die Irrtumswahrscheinlichkeiten können direkt in EXCEL berechnet werden. Dafür wird in eine Zelle die Formel "=CHIVERT(berechneter Chi-Quadrat-Wert; Freiheitsgrade)" eingegeben, in unserem Fall also "=CHIVERT(3,92;1)", welches das Ergebnis "0,04771" liefert.[28] Diese Irrtumswahrscheinlichkeit ist kleiner als 0,05 und damit knapp signifikant, d. h. die Summe der Abweichungen von einer Gleichverteilung der Phraseologismenkenntnis bei Männern und Frauen ist größer als nach dem Zufall erwartet werden kann. Bei einem solchen Ergebnis muss man also annehmen, dass Frauen den betreffenden Phraseologismus häufiger kennen als Männer.
t-Test
Der t-Test untersucht die Frage, ob es einen signifikanten Unterschied zwischen den Mittelwerten zweier intervallskalierter Stichproben gibt (z. B. kennen Probanden ab 50 mehr Phraseologismen als unter 50-jährige Probanden?). Da wir zwei Gruppen betrachten, ist die unabhängige Variable nominalskaliert.[29]
Voraussetzung für die Durchführung eines t-Tests ist eine Normalverteilung der abhängigen Variablen. Diese ist nicht ganz einfach zu testen.[30] In der Praxis kann man auf einen solchen Test verzichten, wenn die meisten Befragungswerte nicht extrem hoch oder extrem niedrig, sondern im mittleren Bereich zwischen den Extremwerten liegen. Je kleiner die Stichprobe, desto schwieriger ist diese Voraussetzung zu prüfen. Der t-Test sollte unter anderem auch deshalb nicht für kleine Testgruppen (unter 20 Probanden) eingesetzt werden.[31]
In der Praxis wird in der Regel ein t-Test für unabhängige Gruppen durchgeführt, der Daten aus zwei Gruppen (z. B. durchschnittliche Phraseologismenkenntnis in zwei Altersgruppen) untersucht. Tests mit abhängigen Gruppen (zweimalige Befragung derselben Probandengruppe) sind eher selten und sollen daher an dieser Stelle nicht weiter behandelt werden.
Führt man den t-Test in EXCEL (unter dem Menü Extras, Analyse-Funktionen) durch, so hat man die Wahl zwischen unabhängigen Stichproben mit gleichen oder unterschiedlichen Varianzen (Varianz: cf. Abschnitt 3.1). Bei der Einstufung in gleiche oder unterschiedliche Varianzen kann in der Praxis auf einen statistischen Test verzichtet werden,[32] indem bei Unsicherheit in EXCEL einfach beide Tests durchgeführt werden. Mit den Testergebnissen werden auch die Varianzen angezeigt. Wenn eine starke Abweichung der Varianzen beider Gruppen vorliegt (z. B. die Varianzen in der einen Gruppe sind mehr als doppelt so groß wie in der anderen), sollte der Test für unterschiedliche Varianzen gewählt werden, bei einer geringen Abweichung reicht der Test für gleiche Varianzen aus. Im Zweifelsfall ist die Annahme unterschiedlicher Varianzen zu empfehlen.
Ebenfalls zu den Testergebnissen gehören zwei unterschiedliche Irrtumswahrscheinlichkeiten, (p-Werte) für einen einseitigen bzw. einen zweiseitigen t-Test. Diese Unterscheidung berücksichtigt bei der Berechnung, ob vor der Analyse ein Unterschied nur in eine bestimmte Richtung erwartet wird (z. B. die älteren Altersgruppen kennen aufgrund ihrer Erfahrung mehr Einträge des tradierten Sprichwortschatzes als jüngere) oder in beide Richtungen gehen kann, d. h. wenn man vorher nicht vermutet, welche Gruppe höhere Werte aufweisen wird. Im Zweifelsfall testet man zweiseitig. Es ist wichtig, dass bei einem einseitigen Test vor dem Sichten der Daten (nicht im Nachhinein) ein begründeter Verdacht besteht, dass eine bestimmte Gruppe einen höheren Mittelwert erzielt. Eine solche gerichtete Erwartung muss dann auch in der Beschreibung der Methoden erklärt werden.
EXCEL zeigt nach dem t-Test in seiner Ergebnistabelle sowohl die Varianzen beider Gruppen, als auch die Freiheitsgrade des Tests und den Wert für die Irrtumswahrscheinlichkeit (p) an. Dieser gibt an, mit welcher Wahrscheinlichkeit der festgestellte Unterschied auf einen Zufall zurückgeführt werden kann.
Beispiel (für 2 unabhängige Gruppen):
Es soll die Hypothese geprüft werden, dass ältere Probanden eine durchschnittlich höhere Sprichwortkenntnis haben. Anhand eines Fragebogens mit 75 Sprichwörtern werden 10 Probanden unter 50 Jahren und 10 Probanden ab 50 befragt. Das Ergebnis der Befragung weist für die ab 50-Jährigen Werte zwischen 59 und 69 bekannten Sprichwörtern und für die unter 50-Jährigen Werte zwischen 54 und 64 auf (cf. die zwei linken Spalten in Tabelle 4).
Da von zwei verschiedenen Probandengruppen (mit unterschiedlichem Alter) ausgegangen wird, ist ein t-Test für zwei unabhängige Gruppen zu verwenden. Da weiterhin anhand früherer Untersuchungsergebnisse begründet angenommen wird, dass die älteren Probanden eine größere Zahl von Sprichwörtern kennen, wird ein einseitiger t-Test durchgeführt.
Wenn man in EXCEL (Extras, Analyse-Funktionen, Zweistichproben t-Test: Gleicher Varianzen[33]) einen t-Test durchführt, erhält man die in Tabelle 4 wiedergegebene Ergebnistabelle. Aus der Auswertung geht hervor, dass die Daten beider Gruppen eine ähnliche Streuung haben, also gleiche Varianzen angenommen werden können.
| Ab 50-Jährige |
Unter 50-Jährige |
|
|||
| 59 |
54 |
Zweistichproben t-Test unter der Annahme gleicher Varianzen |
|||
| 62 |
57 |
||||
| 64 |
59 |
|
Variable 1 |
Variable 2 |
|
| 64 |
59 |
Mittelwert |
65 |
59.8 |
|
| 64 |
59 |
Varianz |
9.56 |
8.18 |
|
| 65 |
60 |
Beobachtungen |
10 |
10 |
|
| 67 |
62 |
Gepoolte Varianz |
8.87 |
||
| 68 |
63 |
Hypothetische Differenz der Mittelwerte |
0 |
||
| 68 |
63 |
Freiheitsgrade (df) |
18 |
||
| 69 |
62 |
t-Statistik |
3.905 |
||
| P(T<=t) einseitig |
0.00052 |
||||
| Kritischer t-Wert bei einseitigem t-Test |
1.734 |
||||
| P(T<=t) zweiseitig |
0.00104 |
||||
| Kritischer t-Wert bei zweiseitigem t-Test |
2.101 |
||||
Tabelle 4: Stichprobenwerte und Testergebnis zum t-Test (mit 2 unabhängigen Gruppen) (EXCEL)
Weiterhin ergibt sich eine einseitige Irrtumswahrscheinlichkeit von p = 0,00052. Dieses Ergebnis ist als hochsignifikant zu betrachten, da der Unterschied zwischen den zwei Gruppen mit 0,052 %iger Wahrscheinlichkeit nicht dem Zufall zuzuschreiben ist. Die Hypothese, dass ab 50-jährige Probanden durchschnittlich mehr Phraseologismen kennen als unter 50-jährige, wird durch diesen Test bestätigt.
Varianzanalyse (analysis of variance - ANOVA)[34]
Die Varianzanalyse testet, ob zwischen mehreren intervallskalierten Stichproben Unterschiede bestehen. Die Varianzanalyse ist der komplexeste der bisher vorgestellten Tests und bietet zugleich die bisher größten Anwendungsmöglichkeiten:
Erstens kann anhand einer Varianzanalyse untersucht werden, ob es einen signifikanten Unterschied zwischen den Mittelwerten von mehr als zwei Stichproben gibt (z. B.: Unterschiede in der Phraseologismenkenntnis von Deutschen, Österreichern und Schweizern). In einer Varianzanalyse wird die Streuung der Werte innerhalb der Gruppen (d. h. wie stark streuen die Werte der Deutschen, wie stark die der Österreicher und wie stark die der Schweizer?) mit der Streuung der Werte zwischen den Gruppen (d. h. wie groß sind die Unterschiede zwischen Deutschen, Österreichern und Schweizern?) verglichen. Wenn die Streuung zwischen den Gruppen größer ist als die Streuung innerhalb der Gruppen, schließt man daraus, dass sich die Gruppen signifikant unterscheiden. Man könnte in dieser Hinsicht von einem erweiterten t-Test mit mehr als zwei Gruppen sprechen.
Zweitens kann in einer Varianzanalyse mehr als ein Faktor, d. h. mehr als eine unabhängige Variable, untersucht werden. Z. B. kann zusätzlich zum Faktor Alter (wie beim t-Test) gleichzeitig der Einfluss des Geschlechts, der Ausbildung und des Wohnortes auf die Kenntnis von Phraseologismen geprüft werden. Je nach Anzahl dieser Faktoren ist eine ein-, zwei- oder mehrfaktorielle Varianzanalyse durchzuführen.
Drittens kann die Varianzanalyse darüber hinaus Aussagen zu Interaktionen, d. h. der gegenseitigen Beeinflussung der untersuchten Faktoren, treffen. Eine Interaktion liegt dann vor, wenn ein Faktor in Anwesenheit eines anderen ein anderes Ergebnis liefert, als wenn dieser zweite Faktor fehlt. Zum Beispiel könnte sich der Bildungsstand in verschiedenen Altersgruppen unterschiedlich auf die Sprichwortkenntnis auswirken (so könnten sich junge Universitätsabsolventen hinsichtlich der Sprichwortkenntnis nicht von Nicht-Universitätsabsolventen unterscheiden, während bei älteren Probanden ein Unterschied festzustellen ist). Auf die Gefahren schwerwiegender Missinterpretationen bei Missachtung der Interaktionen wiesen bereits Grotjahn/Grzybek (2000: 125) hin. Trotzdem ist diese Möglichkeit bei der Auswertung phraseologischer Befragungen bisher vernachlässigt worden.
Für die Varianzanalyse sind wie beim t-Test eine Normalverteilung der Daten[35] und außerdem eine Gleichheit der Varianzen der Stichproben Voraussetzung. Bei diesem Test ist besonders zu berücksichtigen, dass die Zahl der erforderlichen Probanden umso größer sein muss, je komplexer das Versuchsdesign ist. Soll z. B. der Einfluss der vier Faktoren Alter (in 4 Stufen: < 30, 31-40, 41-50, >50 Jahre), Geschlecht (in 2 Stufen: männlich, weiblich), Ausbildung (in 2 Stufen: studiert, nicht studiert) und Wohnort (in 2 Stufen: Deutschland, Schweiz) untersucht werden, so müssen für alle möglichen Kombinationen (4*2*2*2 = 32) ausreichend viele Probanden zur Verfügung stehen (z. B. bei mindestens 10 Probanden und Kombination wären dies in diesem Fall mindestens 320 Probanden).
Die ein- und zweifaktorielle Varianzanalyse können ebenfalls in EXCEL (Extras, Analyse-Funktionen) durchgeführt werden. Für die Auswertung komplexerer Versuchsdesigns (mehrfaktorielle Varianzanalyse) müssen Statistikprogramme herangezogen werden.
Beispiel (für eine einfaktorielle Varianzanalyse):
Geprüft werden soll die Hypothese, dass der Faktor Wohnland einen Einfluss auf die Phraseologismenkenntnis hat. Es wurde daher je 10 Probanden aus Deutschland, der Schweiz und Österreich eine Liste mit 120 Phraseologismen vorgelegt, auf der die ihnen bekannten anzukreuzen waren. Die Probanden kannten aus diesem Korpus folgende Phraseologismen:
|
Deutsche |
Schweizer |
Österreicher |
|
72 |
62 |
81 |
|
87 |
76 |
87 |
|
69 |
68 |
74 |
|
78 |
72 |
86 |
|
82 |
71 |
79 |
|
73 |
69 |
82 |
|
74 |
60 |
89 |
|
81 |
75 |
91 |
|
80 |
62 |
78 |
|
71 |
69 |
86 |
Tabelle 5: Stichprobenwerte zum Varianzanalyse-Beispiel
Nach Eingabe der Werte wird in EXCEL (Extras, Analyse-Funktionen) eine einfaktorielle Varianzanalyse durchgeführt. Folgende Werte werden angezeigt:
Anova: Einfaktorielle Varianzanalyse
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tabelle 6: Testergebnis zur Varianzanalyse (EXCEL)
Aus dem p-Wert von 0,000011 ergibt sich, dass diese drei Stichproben hinsichtlich der Phraseologismenkenntnis hochsignifikant voneinander abweichen. Die Varianzanalyse testet nur, ob alle Stichproben gleich sind (Nullhypothese H0) oder nicht (Alternativhypothese H1). Wenn man wissen möchte, welche der untersuchten Stichproben sich voneinander unterscheiden, muss man nach der Varianzanalyse sogenannte Post-hoc-Tests durchführen. Diese sind in EXCEL nicht möglich, hierfür muss man auf Statistikprogramme zurückgreifen.
Regressionsanalyse
Eine Regressionsanalyse untersucht die Frage, ob zwei intervallskalierte Datengruppen miteinander in Beziehung stehen (z. B. hat das Alter (in Jahren) eine Auswirkung auf die Phraseologismenkenntnis?).[36]
Voraussetzung für die Regressionsanalyse ist, dass zwischen den zwei Datengruppen in etwa ein linearer Zusammenhang besteht (d. h. dass die Punkte nicht deutlich eine Kurve beschreiben).[37] Am deutlichsten wird eine solche Beziehung, wenn die Versuchsergebnisse in einem Diagramm dargestellt werden.
Beispiel:
Es soll die Hypothese geprüft werden, dass das Alter einen Einfluss auf die Phraseologismenkenntnis hat. Dafür werden 10 Probanden im Alter zwischen 28 und 73 Jahren gebeten, anzugeben, welche der vorgegebenen 120 Phraseologismen sie kennen.
In Tabelle 7 werden die Befragungsergebnisse aufgeführt.
|
Alter |
Kenntnis |
|
27 |
71 |
|
34 |
76 |
|
36 |
82 |
|
41 |
85 |
|
47 |
87 |
|
52 |
100 |
|
56 |
98 |
|
64 |
105 |
|
68 |
109 |
|
73 |
108 |
Tabelle 7: Befragungsergebnisse für Regressionsanalyse
Stellt man die Versuchsergebnisse grafisch dar,[38] ergibt sich folgendes Diagramm:
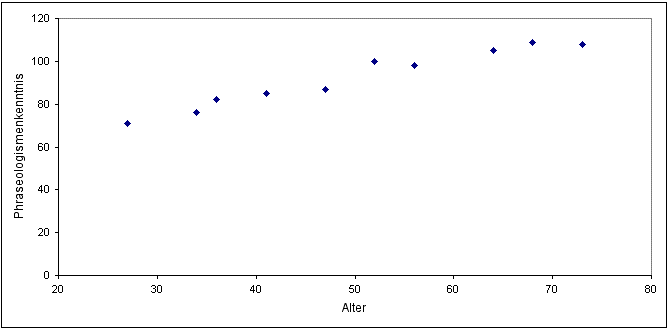
Abbildung 1: Grafische Darstellung der Ergebnisse des Beispiels zur Regressionsanalyse
Eine Regression legt nun eine Grade durch die gemessenen Punkte, so dass die quadrierte Summe der Abstände der Punkte von der Graden minimal ist. Das heißt, dass die Streuung der Punkte um die Grade möglichst gering ist und die Grade damit möglichst gut den Verlauf der Punkte widerspiegelt. Die Grade wird mit folgender Gleichung beschrieben:
wobei b der Steigung der Graden entspricht und a dem Schnittpunkt der Graden mit der y-Achse.[39]
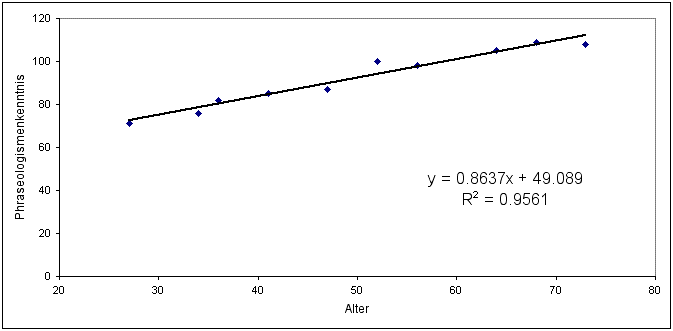
Abbildung 2: Regressionsgrade zum Beispiel zur Regressionsanalyse
Für die Phraseologie sind i. d. R. zwei Fragestellungen der Regressionsanalyse von Interesse:
Erstens: Hat die unabhängige Variable (im Beispiel das Alter) einen signifikanten Einfluss auf die abhängige Variable (im Beispiel die Phraseologismenkenntnis)? Dieser Einfluss kann sowohl positiv (je älter desto mehr Phraseologismen sind bekannt, b = positiv) als auch negativ (je älter desto weniger, b = negativ) sein. Wenn die unabhängige Variable keinen Einfluss auf die abhängige Variable hat, sollte die Steigung der Graden nahe bei Null liegen, d. h. die Grade verliefe in etwa parallel zur x-Achse. Die Regressionsanalyse testet, ob sich b signifikant von Null unterscheidet und damit ein signifikanter Einfluss vorliegt.
Zweitens: Wie gut wird die abhängige Variable durch die unabhängige Variable erklärt? Die Stärke des Einflusses wird im Bestimmtheitsmaß R2 angegeben[40] und zeigt an, welcher Anteil der Variabilität (zwischen 0 und 100 %) sich durch den Einfluss der unabhängigen Variablen erklären lässt. Wenn die Datenpunkte sehr stark um die Grade streuen, erklärt die unabhängige Variable nur einen geringen Teil der Variabilität in den Datenpunkten, wenn die Punkte nahe an der Grade liegen, lässt sich ein großer Teil der Variabilität durch sie erklären.
Eine Regressionsanalyse kann ebenfalls in EXCEL durchgeführt werden.[41] Das Ergebnis sieht wie folgt aus:
ANOVA
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Tabelle 8: Ergebnis des Beispiels zur Regressionsanalyse (EXCEL)
Im unteren Teil der Tabelle kann man die Koeffizienten der Gradengleichung ablesen: Der Schnittpunkt mit der y-Achse a = 49,09 und die Steigung b = 0,86 (siehe auch Formel in Abb. 2). Im angegebenen hypothetischen Beispiel ist die Steigung, d. h. der Einfluss der unabhängigen auf die abhängige Variable (Alter auf die Phraseologismenkenntnis) hochsignifikant (p < 0,001), wobei sich laut Bestimmtheitsmaß knapp 96 % der Variabilität oder Streuung der Bekanntheitswerte um die Grade durch die unabhängige Variable Alter erklären lässt. Weiter kann man an der Steigung b ablesen, dass die Probanden mit jedem Lebensjahr durchschnittlich 0,86 Phraseologismen mehr kennen.
Man beachte: Das Ergebnis einer Regressionsanalyse zeigt nur an, ob zwei Datengruppen korrelieren, d. h. einen vergleichbaren Verlauf nehmen. Aus einer signifikanten Regression lässt sich keine Kausalität ableiten, d. h. wenn die Phraseologismenkenntnis mit zunehmendem Alter steigt, bedeutet dies nicht zwangsläufig, dass das Alter der Probanden für diese Steigerung verantwortlich ist. Dieses Ergebnis könnte auch beispielsweise darauf zurückgeführt werden, dass ältere Probanden besser ausgebildet sind als jüngere und die bessere Ausbildung diesen höheren Kenntnisstand bedingt.
Wie die Abschnitte 2. und 3. gezeigt haben, kann sowohl bei den phraseologischen Fragestellungen als auch bei den statistischen Tests generell zwischen Ein- und Mehrdimensionalität unterschieden werden.
Eindimensionale Fragestellungen können beispielsweise auf die Beschreibung eines getesteten Korpus (bei einer Befragung mit vorgegebenen Phraseologismen), auf die Zusammenstellung eines Korpus (bei einer Befragung ohne vorgegebene Formen), auf das Verständnis oder den Erwerb von Phraseologismen zielen. Bei der Darstellung können die Methoden der deskriptiven Statistik (Tabellen, Grafiken, Maßzahlen) die Ergebnisse veranschaulichen.
Mehrdimensionale Fragestellungen zielen darauf ab, mindestens zwei Variablen zueinander in Beziehung zu setzen. Um zu testen, ob die Unterschiede in den Befragungsergebnissen tatsächlich auf einen Unterschied zwischen zwei oder mehr Gruppen oder auf den Zufall (begründet in der Probandenauswahl oder Korpuszusammenstellung) zurückzuführen sind, müssen die Methoden der schließenden Statistik zur Hilfe genommen werden.
Der Weg von der Fragestellung einer empirischen phraseologischen Untersuchung bis zum Testergebnis und seiner Deutung wird in Tabelle 9 dargestellt. In der linken Spalte sind die Tätigkeiten, in der rechten Spalte die Fachbereiche, denen die einzelnen Schritte zugerechnet werden können, dargestellt.
|
Praktisches Vorgehen |
Angesprochener Fachbereich |
|
1. Fragestellung der Untersuchung |
Phraseologischer Ausgangspunkt |
|
2. Hypothesenformulierung |
Übergang Phraseologie - Statistik |
|
3. Wahl des Tests (cf. Tabelle 3) |
Statistik: Theorie |
|
4. Planung der Befragung (evtl. Vortest) |
Empirie: Theorie |
|
5. Durchführung der Befragung |
Empirie: Praxis |
|
5. Datenaufbereitung + Durchführung des Tests |
Statistik: Praxis |
|
6. Testergebnis be- oder widerlegt Hypothese |
Übergang Statistik - Phraseologie |
|
7. Bedeutung des Ergebnisses |
Phraseologisches Ergebnis |
Tabelle 9: Von der Fragestellung zur Deutung des Ergebnisses
Aus dieser Tabelle ist ersichtlich, dass die phraseologische Fragestellung den Ausgangspunkt eines quantitativen Ansatzes darstellt. Mit der Formulierung einer begründeten Hypothese wird die Grundlage für eine statistische Untersuchung gelegt.
Aufgrund dieser These ist zu bestimmen, mit welcher abhängigen und welcher/welchen unabhängigen Variablen gearbeitet wird und wie diese skaliert sein sollen. In Tabelle 3 ist dargestellt, welcher Test nach diesen Vorentscheidungen zu wählen ist.
Abhängig von der phraseologischen Fragestellung und dem gewählten statistischen Test wird die Befragung geplant. Auf dieser Stufe sollte auch eine Abschätzung stattfinden, wie viele Probanden notwendig sind, um die Fragestellung beantworten zu können. Um etwaige Probleme bereits im Vorfeld zu beseitigen, ist es empfehlenswert, einen Vortest durchzuführen und die Befragung aufgrund seiner Ergebnisse anzupassen.
Nach diesen gründlichen Vorarbeiten wird die Befragung der Probanden durchgeführt.
Anhand der eingegangenen Fragebögen werden die Daten aufbereitet (z. B. elektronische Erfassung der Probandendaten, Darstellung der Daten anhand von Methoden der deskriptiven Statistik) und schließlich - wie in Abschnitt 3 beschrieben - die Tests durchgeführt.
Die Testergebnisse zeigen an, ob die anfänglich aufgestellte Hypothese bestätigt werden kann. Damit ist die Auswertung der Befragung nach statistischen Gesichtspunkten abgeschlossen und mit der Positionierung oder Deutung des Ergebnisses aus phraseologischer Perspektive kehren wir in den Bereich der Sprachwissenschaft zurück.
Die Statistik wird also, ebenso wie die empirische Methodik, als Mittel der Erkenntnisgewinnung im Bereich der Phraseologie genutzt. Das Ziel der Statistik, nämlich ausgehend von einer Testgruppe Rückschlüsse auf eine Gesamtgruppe zu ziehen, gilt ebenso für phraseologische Befragungen. Die Befragung von 500 repräsentativen Probanden soll über diese kleine Testgruppe hinaus Aussagen über einen größeren Personenkreis, evtl. über die Gesamtgruppe der Muttersprachler, zulassen.
Die Notwendigkeit der Einbeziehung statistischer Methoden für die Auswertung phraseologischer Befragungen wurde bisher nicht bestritten. Die Divergenzen der Ergebnisse bisheriger Untersuchungen ließen sich durch eine strikte Einhaltung der Testbedingungen und eine korrekte Durchführung der Tests relativieren.[42]
Ich habe auf den vorangehenden Seiten gezeigt, dass die Auswahl des jeweiligen Tests nach klaren und nachvollziehbaren Kriterien erfolgen muss. Gleichzeitig habe ich einen ersten Einblick in die Anwendung dieses Auswahlverfahrens ermöglicht.
Was unter den Möglichkeiten der dargestellten Tests in Zukunft besonderes Gewicht finden sollte, ist die Berücksichtigung von Interaktionen zwischen verschiedenen Faktoren (in der Varianzanalyse), um die gegenseitige Abhängigkeit von Faktoren aufzudecken und so vor Fehlinterpretationen zu schützen.
Es ist wünschenswert, dass die statistische Methodik bei empirischen phraseologischen Befragungen wie auch in anderen empirischen Bereichen der Sprachwissenschaft ebenso zum allgemein anerkannten Standardverfahren wird wie beispielsweise in den Sozial- und Naturwissenschaften.
Anmerkung
Auf Anfrage wird gern eine EXCEL-Arbeitsmappe mit Beispielen zu diesem Artikel
versandt (britta.juska-bacher@access.unizh.ch bzw. bjuskabacher@hotmail.com).
1 Dies sowohl in Form der Einholung metasprachlicher Auskünfte von Probanden zu ihrer Phraseologismenkenntnis, -verwendung, -bewertung (cf. Häcki Buhofer/Burger 1994) und ihrem Verständnis als auch in Form von Ergänzungstests (cf. Grzybek 1991). [zurück]
2 Cf. Grotjahn/Grzybek (2000: 121f) [zurück]
3 Cf. Grzybek (1991) und Häcki Buhofer/Burger (1994). [zurück]
4 Dabei lassen sich die vorgestellten Methoden problemlos auch auf produktions- und rezeptionsorientierte Untersuchungen anderer linguistischer Bereiche übertragen. [zurück]
5 Cf. Friedrich Vogel (1997): Beschreibende und schließende Statistik. München/Wien: Oldenbourg. [zurück]
6 Bei der ebenfalls in diesem Themenheft enthaltenen Untersuchung handelt es sich um eine Kombination aus Befragung und Korpusanalyse. Für den vorliegenden Artikel ist nur der Befragungsteil von Interesse. [zurück]
7 Denkbar sind auch Untersuchungen, die nicht von korpus-, sondern von probandenorientierten Daten ausgehen und ihre Beeinflussung durch in der Befragung erfasste Faktoren untersuchen (z. B. Einfluss des Alters oder Geschlechts auf den Spracherwerb). Diese fehlen bisher im deutschen Sprachraum. [zurück]
8 Bei der Beschreibung der statistischen Grundlagen sowie der verschiedenen Tests stütze ich mich auf folgende Literatur: Albert/Koster (2002), Nachtigall/Wirtz (1998) und Wirtz/Nachtigall (1998) aus dem Bereich der Sprachwissenschaft, Atteslander (2003) aus dem Bereich der Soziologie sowie Bosch (1997), Kähler (2005), Köhler/Schachtel/Voleske (1996) aus der Statistik bzw. Biostatistik. [zurück]
9 Zur Repräsentativität von Stichproben cf. auch Gabler (1996). [zurück]
10 Selbst eine Auswahl der Probanden nach Telefonbuch oder übers Internet stellt streng genommen keine zufällige Auswahl da, da nicht alle Probanden der Gesamtgruppe (beispielsweise des deutschen Sprachraums) die gleiche Chance haben, erreicht zu werden, i. d. R. stellen ja nicht nur Personen mit Telefonanschluss oder Internetzugang, sondern beispielsweise alle Bewohner eines Landes die Gesamtgruppe dar. [zurück]
11 Die Beispiele dieses Kapitels werden im Tabellenkalkulationsprogramm EXCEL vorgerechnet und finden sich in der EXCEL-Arbeitsmappe zu diesem Artikel auf dem Tabellenblatt "Deskriptive Statistik". VORSICHT: In diesem Artikel wird das Komma als Dezimalzeichen verwendet, je nach Voreinstellung muss aber in EXCEL das Komma oder der Punkt verwendet werden. [zurück]
12 Die kleine Stichprobenzahl wurde in diesem Beispiel aus Gründen der leichteren Darstellbarkeit der Berechnung gewählt und reicht selbstverständlich für Rückschlüsse auf die Gesamtgruppe nicht aus. [zurück]
13 Zur Berechnung des Mittelwerts kann man auch, besonders bei großen Datenmengen, auf die in EXCEL vorhandene Funktion MITTELWERT zurückgreifen: Anklicken einer leeren Zelle, in die der Mittelwert geschrieben werden soll, dann über das Menü Einfügen, Funktion ..., Funktionskategorie: Statistik, Name der Funktion: MITTELWERT. Es erscheint ein Fenster, in dem man den Bereich angeben muss, in dem die Daten stehen, deren Mittelwert berechnet werden soll. Alternativ kann man auch die Formel direkt in eine Zelle eintippen (ohne Anführungszeichen, cf. EXCEL-Arbeitsmappe zu diesem Artikel): "=MITTELWERT(Anfangszelle:Endzelle)". [zurück]
14 Auch diese Funktion ist in EXCEL bereits vorhanden: Menü Einfügen, Funktion ..., Funktionskategorie: Statistik, Name der Funktion: STABW. Wieder erscheint ein Fenster, in dem man den Bereich angeben muss, in dem die Daten stehen, deren Standardabweichung berechnet werden soll. Oder direkt: "=STABW(Anfangszelle:Endzelle)". [zurück]
15 Auch die Varianz lässt sich in EXCEL errechnen (Menü Einfügen, Funktion ..., Funktionskategorie: Statistik, Name der Funktion: VARIANZ). [zurück]
16 Auch als analytische oder induktive Statistik bezeichnet [zurück]
17 Zur Begrifflichkeit unabhängige und abhängige Variable s. u. [zurück]
18 Dabei ist es wichtig, deutlich zwischen dem alltagssprachlichen und dem statistischen Fachterminus Signifikanz zu unterscheiden. Während der alltagssprachliche Begriff für "Bedeutsamkeit" oder "Wichtigkeit" steht (cf. Wahrig), gibt ein signifikantes Ergebnis in der Statistik an, in wie weit ein aus der Datenanalyse abzeichnendes Muster mit einer gewissen Wahrscheinlichkeit als tatsächliches Charakteristikum dieses Systems oder als zufällig zu bewerten ist. [zurück]
19 Die Empfehlung, immer möglichst große Probandenzahlen zu verwenden, gilt mit gewissen Einschränkungen. Für extrem große Probandenzahlen gilt nämlich, dass signifikante Unterschiede immer wahrscheinlicher werden, selbst wenn der absolute Unterschied der Gruppen klein ist. Irgendwann stellt sich die Frage, welche praktische Bedeutung eine so geringe Differenz noch hat, auch wenn sie signifikant ist. Dieser Punkt wird hier allerdings vernachlässigt, da phraseologische Untersuchungen in der Praxis eher mit zu kleinen Stichprobengrößen zu kämpfen haben. [zurück]
20 VORSICHT: Für alle statistischen Tests gilt, dass man bei Irrtumswahrscheinlichkeiten < 0,05 schliessen kann, dass signifikante Unterschiede vorliegen. Umgekehrt darf man allerdings nicht folgern, dass bei Irrtumswahrscheinlichkeiten > 0,05 keine Unterschiede vorhanden sind, da man nicht entscheiden kann, ob keine Unterschiede festgestellt wurden, weil z. B. die Stichprobe zu klein war, oder ob tatsächlich keine signifikanten Unterschiede vorliegen. [zurück]
21 Man sollte sich bewusst sein, dass bei den meisten Fragestellungen in der Phraseologie auch mit statistischen Tests keine zwingende kausale, sondern nur eine korrelative Beziehung zwischen der abhängigen und der/den unabhängigen Variablen abgeleitet werden kann. D. h. die unabhängige Variable muss nicht unbedingt die Ursache für das beobachtete Muster darstellen. Eine kausale Abhängigkeit zu zeigen, wäre nur möglich, wenn man in einem Experiment die zu untersuchenden unabhängigen Variablen den Probanden in einer Zufallsauswahl zuordnen würde. Dies ist leider nur in den seltensten Fällen möglich; man kann z. B. das Alter nicht den Teilnehmern einer Umfrage zuordnen. Wenn andere Faktoren mit der untersuchten unabhängigen Variablen korrelieren (z. B. ältere Leute zugleich eine bessere Ausbildung haben), kann man nicht feststellen, ob diese nicht einen stärkeren Einfluss auf die abhängige Variable ausüben. [zurück]
22 Ein drittes, allerdings weniger häufiges Skalierungsniveau stellen ordinalskalierte Daten dar. Hier werden die gemessenen Daten nach Größe, Stärke oder Intensität in eine Rangliste gestellt (z. B. Rangliste der Bekanntheit verschiedener Phraseologismen, Einordnung der Phraseologismen in verschiedene Verwendungsstufen von sehr häufig - häufig - mittel - selten - nie). [zurück]
23 Die logistische Regression wird wegen ihrer Komplexität und ihres eher seltenen Bedarfs in diesem Artikel (wie auch in den aufgeführten Statistikbüchern) nicht behandelt. [zurück]
24 EXCEL ab Version 2000 bietet als Add-In die sog. Analyse-Funktionen an. Diese müssen für die Durchführung der meisten hier beschriebenen Tests im Programm selbst aktiviert werden, indem man unter dem Menü Extras, Add-Ins-Manager die Analyse-Funktionen ankreuzt. Danach kann man diese vom Menü Extras aufrufen (unterster Eintrag). [zurück]
25 Wenn eine Liste mehrere Phraseologismen enthält, ist für jeden einzelnen Phraseologismus ein Chi-Quadrat-Test durchzuführen. Allerdings muss bei mehreren Tests die Irrtumswahrscheinlichkeit von p = 0,05 angepasst werden, denn diese besagt ja, dass man in Kauf nimmt, sich in einem von 20 Fällen zu irren. Wenn viele Tests durchgeführt werden, besteht die Gefahr, dass man - auch wenn die Gruppen in der Realität keine Unterschiede aufweisen - doch zufällig signifikante Unterschiede findet und damit falsche Schlussfolgerungen zieht. Um diesen Fehler zu vermeiden, kann man die Irrtumswahrscheinlichkeit von p = 0,05 durch die Anzahl durchgeführter Tests teilen (Bonferroni-Korrektur) und erhält so die korrigierte Irrtumswahrscheinlichkeit, die noch einen signifikanten Unterschied ausweisen soll. Z. B. bei 5 durchgeführten Tests ergibt sich pkorrigiert = 0,05/5 = 0,01, d. h. jeder der 5 durchgeführten Tests kann nur dann als signifikant gelten, wenn er eine Irrtumswahrscheinlichkeit von p < 0,01 ausweist. [zurück]
26 Für den Chi-Quadrat-Test darf die erwartete Häufigkeit in keiner der Zellen der Tabelle kleiner als 5 sein, ansonsten ist anstelle des angenäherten Tests ein exakter Test durchzuführen. [zurück]
27 Freiheitsgrade sind ein abstraktes Konstrukt in der Statistik und geben die Anzahl derjenigen Werte an, die in einem Test frei variieren können. Sie sind beim Chi-Quadrat-Test von der Anzahl gewählter Klassen und bei den anderen Tests von der Probandenzahl abhängig. Generell gilt: je mehr Freiheitsgrade, desto leichter lässt sich ein signifikanter Unterschied finden. [zurück]
28 Man kann dies auch über das Menü Einfügen, Funktion ..., Funktionskategorie: Statistik, Name der Funktion: CHIVERT tun. [zurück]
29 Wenn man mehr als zwei Stichproben betrachtet (z. B. Gruppe 1: unter 30-Jährige, Gruppe 2: 30- bis 50-Jährige und Gruppe 3: über 50-Jährige), ist statt eines t-Tests eine Varianzanalyse durchzuführen (s. u.). Es ist nicht erlaubt, mehrere t-Tests nacheinander mit denselben Stichproben durchzuführen (z. B. Gruppe 1 gegen Gruppe 2, 1 gegen 3 und 2 gegen 3), da man die Wahrscheinlichkeit erhöht, dass zufällige Unterschiede zwischen den Gruppen als signifikant ausgewiesen werden. Aus demselben Grund darf man dieselben Stichproben nicht nach mehreren Faktoren (z. B. Alter, Geschlecht, Ausbildung) mit wiederholten t-Tests auswerten. Für die Untersuchung mehrerer Faktoren ist eine mehrfaktorielle Varianzanalyse durchzuführen. [zurück]
30 Tests auf Normalverteilung werden in diesem Artikel nicht besprochen, sind aber in den einschlägigen Statistikprogrammen vorhanden. Moderate Abweichungen von der Normalverteilung der Daten haben bei den angegebenen Tests nur einen geringen Einfluss auf das Ergebnis. Der Test ist daher in erster Linie bei knapp signifikanten oder nicht-signifikanten Ergebnissen wichtig, weniger bei deutlich signifikanten Ergebnissen. [zurück]
31 Da eine Probandenzahl von < 20 dem Postulat der möglichst großen Stichprobe häufig nicht gerecht wird, werden die alternativ einzusetzenden Tests hier nicht ausführlicher besprochen. Es sei nur darauf hingewiesen, dass in solchen Fällen der U-Test von Mann und Whitney als Alternative zum t-Test benutzt werden kann, cf. u.a. Bosch (1997: 188-190); Kähler (1995: 283-298); Köhler/Schachtel/Voleske (1996: 101-104); Nachtigall/Wirz (1998: 141-147) oder Schlobinski (1996: 155-158). [zurück]
32 Den gibt es natürlich: Ein F-Test oder Varianzquotiententest (cf. Köchler/Schachtel/Voleske 1996: 100f oder Nachtigall/Wirtz 1998: 125-127). [zurück]
33 In EXCEL: Menü Extras, Analyse-Funktionen, Zweistichproben t-Test: Gleicher Varianzen. Es erscheint ein Fenster, in dem man den Datenbereich der ersten Gruppe angeben muss (im Beispiel in der EXCEL-Arbeitsmappe zu diesem Artikel die Zellen A3:A14) und darunter den Datenbereich für die zweite Gruppe (B3:B14). Da sich die Überschriften im Datenbereich befinden, kreuzt man das Feld "Beschriftungen" an. Zum Schluss muss noch der Ausgabebereich gewählt werden, wenn man die Ergebnisse auf demselben Tabellenblatt haben möchte (im Beispiel: A18). Zum Abschluss auf OK drücken. [zurück]
34 Neben den bereits genannten Statistikbüchern cf. speziell zur Varianzanalyse auch Rietveld/Van Hout (2005). [zurück]
35 Liegt keine Normalverteilung vor, ist im einfaktoriellen Fall auf den Kruskal-Wallis-Test (H-Test) zurückzugreifen (cf. Köhler/Schachtel/Voleske 1996: 178-183), für eine zweifaktorielle, nicht normalverteilte Analyse liegt bisher kein geeigneter, nicht-parametrischer Test vor. Generell ist anzumerken, dass die Varianzanalyse recht robust gegenüber Abweichungen von der Normalverteilung ist, d. h. dass moderate Abweichungen i. d. R. keine größeren Auswirkungen auf das Ergebnis haben. Es besteht weiterhin die Möglichkeit, die Daten vor der Analyse zu transformieren, um sie so in eine normalverteilte Form zu bringen. Mögliche Transformationen können in Statistikbüchern nachgelesen werden. [zurück]
36 Bei mehr als zwei Variablen ist eine multiple Regression durchzuführen. Diese ist in EXCEL nicht möglich, hierfür muss man auf Statistikprogramme zurückgreifen. [zurück]
37 Falls die Daten nicht linear verteilt sind, kann in EXCEL statt einer Graden eine Kurve (z. B. logarithmisch, exponentiell) gewählt werden. [zurück]
38 EXCEL: Diagramm-Assistent, Standardtypen, Punkt: (XY). Danach die Schaltfläche Weiter drücken. Als nächstes muss man den Datenbereich angeben (im Beispiel: A3:B13 oder mit der linken Maustaste den Bereich markieren), danach wieder Weiter drücken. Auf den nächsten Seiten kann man das Diagramm noch nach eigenen Wünschen anpassen. [zurück]
39 In EXCEL kann man in einem Punkt-Diagramm eine Trendlinie einfügen, die unserer Regressionsgraden entspricht. Dafür klickt man auf das betreffende Diagramm und wählt aus dem Menü Diagramm, Trendlinie hinzufügen, Typ: linear. Auf der Karteikarte Optionen kann man ankreuzen, ob man die Gleichung und das Bestimmtheitsmaß im Diagramm dargestellt haben möchte. [zurück]
40 Das Bestimmtheitsmaß R2 hängt vom Korrelationskoeffizienten R ab, der die Stärke des linearen Zusammenhangs angibt und maximal den Wert + 1 (ideale positive Korrelation) und minimal den Wert - 1 (negative Korrelation) hat. [zurück]
41 Unter dem Menü Extras, Analyse-Funktionen, Regression anklicken. Nur die Eingabe des Bereichs der x- und der y-Werte ist nötig, der Rest ist optional. [zurück]
42 Im Rahmen der Auswertung einer phraseologischen Befragung im niederländischer Sprachraum (cf. Juska-Bacher 2006a) wurden die statistischen Tests nach der hier vorgestellten Methodik vorgenommen. Da die niederländischen Daten zu einem großräumigeren, sprachvergleichenden Projekt gehören (cf. Juska-Bacher 2006b), ist eine methodische Standardisierung aus Gründen der Vergleichbarkeit besonders wichtig. [zurück]
Albert, Ruth/Koster, Cor J. (2002): Empirie in Linguistik und Sprachlehrforschung. Tübingen.
Atteslander, Peter (2003): Methoden der empirischen Sozialforschung. Berlin/New York.
Bosch, Karl (1997): Elementare Einführung in die angewandte Statistik. Braunschweig.
Buhofer, Annelies (1980): Der Spracherwerb von phraseologischen Wortverbindungen. Frauenfeld/Stuttgart
Ďurčo, Peter (2003): "Unterschiede in der (Un)kenntnis von Sprichwörtern in verschiedenen Lebensaltern". In: Häcki Buhofer, Annelies (ed.): Spracherwerb und Lebensalter. Tübingen/Basel: 293-303. (=Reihe Basler Studien zur deutschen Sprache und Literatur 83).Dürring, Alexia (2004): "Das Phraseologieverständnis von Zweitklässlern - eine empirische Untersuchung". In: Palm-Meister, Christine (ed.): Europhras 2000. Tübingen: 69-78.
Gabler, Siegfried (1996): "Repräsentativität von Stichproben". In: Goebl, Hans et al. (eds.): Kontaktlinguistik. Berlin/New York: 733-737. (=HSK 12.1)
Grotjahn, Rüdiger/Grzybek, Peter (2000): "Methodological remarks on statistical analyses in empirical paremiology". Proverbium 17: 121-132.
Grzybek, Peter (1991): "Sinkendes Kulturgut? Eine empirische Pilotstudie zur Bekanntheit deutscher Sprichwörter". Wirkendes Wort 2/1991: 239-264.
Häcki Buhofer, Annlies/Burger, Harald (1994): "Phraseologismen im Urteil von Sprecherinnen und Sprechern". In: Sandig, Barbara (ed.): Europhras 92. Tendenzen der Phraseologieforschung. Bochum: 1-33.
Juska-Bacher, Britta (2006a): "Zur Bekanntheit und Verwendung von Pieter Bruegels "Sprichwörtern" in der Gegenwart - ein Beitrag zur empirischen Phraseologie des Niederländischen". Proverbium 23. (Im Druck).
Juska-Bacher, Britta (2006b): "Pieter Bruegels Niederländische Sprichwörter als Ausgangspunkt einer kontrastiven phraseologischen Studie." In: Kržišnik, Erika (ed.): Europhras Slovenija 2005. Phraseologie in der Sprachwissenschaft und anderen Disziplinen. (Im Druck).
Kähler, Wolf-Michael (2005): Einführung in die Statistische Datenanalyse. Braunschweig/Wiesbaden.
Köhler, Wolfgang/Schachtel, Gabriel/Voleske, Peter (1996): Biostatistik. Heidelberg.
Nachtigall, Christof/Wirtz, Markus (1998): Wahrscheinlichkeitsrechnung und Inferenzstatistik. Statistische Methoden für Psychologen. Teil 2. Weinheim/München.
Piirainen, Elisabeth (2003): "Es ist noch nicht im Topf, wo's kocht. Zu Idiomen aus dem Raum der ehemaligen DDR". Niederdeutsches Wort 43: 202-219.
Piirainen, Elisabeth (2005): "Europeanism, internationalism or something else? Proposal for a cross-linguistic and cross-cultural research project on widespread idioms in Europe and beyond". Hermes. Journal of Linguistics 35: 45-75.
Rietveld, Toni/van Hout, Roeland (22005): "Quantitive Methods/Quantitative Methoden". In: Ammon, Ulrich et al. (eds.): Soziolinguistik. Berlin/New York: 965-978. (=HSK 3.2).
Schlobinski, Peter (1996): Empirische Sprachwissenschaft. Opladen.
Wirtz, Markus/Nachtigall, Christof (1999): Deskriptive Statistik. Statistische Methoden für Psychologen. Teil 1. Weinheim/München.